Soluciones

1. Al unir las cinco caras triangulares que convergen en cada vértice del icosaedro se forma un pentágono regular. Así que si colocamos el foco frente a un Vértice el contorno de esas cinco Caras formará, en la proyección, un pentágono. Lo mismo sucederá con el Vértice opuesto, el más alejado del foco. Cuando ambos Vértices están alineados con el foco se produce el efecto de la figura: un pentágono inscrito en otro.

2. Al mover el punto rojo el poliedro rota alrededor de la vertical que pasa por su centro. El contorno de la sombra varía, pues cambia la posición de los Vértices respecto al foco.

3. El deslizador amarillo varía el ángulo de luz (más abierto o cerrado) y el deslizador verde la profundidad del plano donde se proyecta el poliedro.

4. Sí, es fácil conseguir que el contorno de la sombra sea heptagonal.

5. Basta tantear hasta conseguir alinear, más o menos, dos Vértices con el foco de luz.

6. En esa posición el plano de proyección se coloca prácticamente perpendicular a la pantalla, así que de la proyección solo vemos un segmento por el que se distribuyen los Nodos (cambiando de posición al rotar el poliedro).

7. Para lograrlo basta alinear el foco de luz con dos Vértices opuestos de una misma Cara del cubo.

8. Para lograrlo basta situar el foco frente al centro de una de las Caras del cubo.

9. Para que solo se vieran cuatro Nodos, tendría que haber cuatro pares de Vértices alineados con el foco. Eso solo es posible colocando el foco a una distancia "infinita", de forma que los rayos de luz sean paralelos.

10. Para lograrlo basta alinear el foco de luz con dos Vértices del tetraedro.

11. Para lograrlo basta alinear el foco de luz con dos Vértices del octaedro.

12. Como nuestra mente tiene mucha más experiencia viendo rotaciones de cuerpos que proyecciones, la ambigüedad de la imagen de la proyección plana en movimiento es reinterpretada, en nuestra percepción, como otra figura espacial (otro poliedro) exterior y semejante al original, que gira con él.

13. Hay tantas Regiones como Caras tiene el tetraedro: cuatro.

14. Hay tantas Regiones como Caras tiene el tetraedro: ocho.

15. En todos los casos hay tantas Regiones como Caras.

16. La igualdad "Regiones + Nodos - Líneas = 2" se cumple porque siempre hay tantas Regiones como Caras, tantos Nodos como Vértices y tantas Líneas como Aristas.

17. Como todos los Nodos están conectados entre sí, la cuenta es sencilla. Hay 4 formas de elegir el primer Nodo (A, B, C o D). Para cada una de esas formas, tenemos 3 formas (quedan tres Vértices libres) de elegir el segundo Nodo. Así que en total tenemos 4x3=12 formas de elegir los dos primeros Nodos. Para cada una de ellas, todavía disponemos de dos formas de elegir el tercer Nodo. Por lo tanto, en total hay 24 caminos posibles (4!).

18. La primera Línea la podemos recorrer de 12 formas distintas (4x3).

19. Eligiendo AB, solo restan dos caminos posibles: ABCD y ABDC. Como todos los Nodos están conectados entre sí, los dos caminos pueden cerrarse formando un circuito cerrado.

20. En total habrá 24 caminos (y también 24 circuitos).

21. Como ahora hay 6 vértices, tenemos 6x5= 30 formas de recorrer la primera Línea.

22. Eligiendo AB como primera Línea, hay 10 caminos posibles: CDFE, CDEF, CEDF, CEFD, DCEF, DFEC, FDCE, FDEC, FEDC y FECD, de los cuales todos menos dos (los acabados en D) permiten el cierre.

23. Por tanto, hay 300 caminos posibles, de los cuales 240 pueden cerrarse en circuitos.

24. Como el cubo tiene 8 Vértices, hay 8x7=56 formas de empezar. Eligiendo como AB una de ellas, solo hay 6 recorridos posibles: CHGDEF, CHGFED, DEEFGH, EDCHGF, EFGDCH y EFGHCD, de los cuales todos menos dos (los acabados en D) permiten el cierre. Así que en total hay 336 caminos y 224 circuitos.

25. Es fácil encontrar una solución, basta con tener cuidado de no formar un circuito antes de tiempo. Un circuito posible es, por ejemplo, ABCDQRSOPFEIJKLHGNMTA:

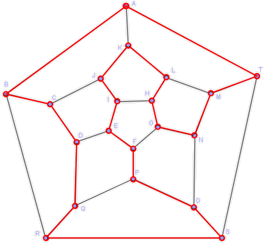
26. Un circuito posible es, por ejemplo, ABCDEFLKGHIJA:

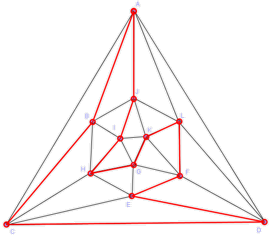
27. Es imposible pasar por todas la Aristas del tetraedro, porque para poder hacerlo los dos Vértices intermedios tendrían que tener "valencia" (número de aristas concurrentes en cada uno de ellos) par. Por la misma razón, es imposible pasar por todas las Aristas del dodecaedro.

28. El único poliedro regular que permite un camino por todas sus Aristas sin repetir ninguna (camino "euleriano") es el octaedro, pues todos sus Vértices tienen valencia par.

29. Como en el octaedro todos los vértices (también el inicial y el final) tienen valencia par, todos los caminos eulerianos serán también circuitos eulerianos, es decir, el Nodo inicial coincidirá con el Nodo final. Uno de estos circuitos es, por ejemplo, ABCAECDEFDBFA.

30. Aunque parezca sorprendente, hay nada menos que 1488 circuitos distintos. Es decir, una vez elegido el vértice de partida (6 posibilidades) y la primera arista (4 posibilidades), para cada una de estas 24 elecciones posibles hay nada menos que 62 circuitos distintos.