Soluciones

1. El valor aproximado de Φ que se encuentra es 1.618.

2. Resolviendo la ecuación:

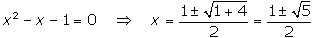
Se obtienen dos soluciones, pero solamente sirve la positiva (buscamos la razón entre dos longitudes). Por tanto el valor exacto del número de oro es:

3. No podemos expresar el valor exacto de Φ en forma decimal. 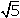es un número irracional, por lo que Φ también es irracional: Φ=1.61803398...

4. La base del rectángulo es el propio segmento y su altura es la parte mayor en que lo dividimos.

5. Las dimensiones son 1 y 0.618, respectivamente. Se cumple que:

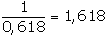
6. La recta trazada sobre la diagonal del rectángulo verde pasa por el vértice superior derecho del rectángulo amarillo. Lo que significa es que tomando como base la suma de la base y la altura de un rectángulo áureo y como altura su base volvemos a obtener un rectángulo áureo.

7. Se comprueba que la tarjeta de crédito tiene unas dimensiones próximas a las de un rectángulo de oro.

8. El ejercicio permite contrastar la respuesta dada en el anterior: los contornos de la tarjeta de crédito y del rectángulo áureo son prácticamente coincidentes. En realidad las dimensiones de una tarjeta de crédito son de 85.60 mm de largo por 53.98 mm de ancho, cuya razón es, aproximadamente, 1.59. La diferencia con un rectángulo áureo es pequeña y difícil de apreciar con estos medios.

9. El DNI tiene las mismas dimensiones que las tarjetas de crédito, por lo que también se aproxima bastante a un rectángulo de oro.

10. La foto no es un rectángulo áureo. También se aproxima mucho a un rectángulo áureo el cuadro de "La última cena" de Salvador Dalí.

11. Basta observar que la relación que se muestra bajo los rectángulos expresa que sus lados correspondientes son proporcionales, por tanto ambos rectángulos son semejantes y, en consecuencia, los dos son rectángulos áureos.

12.  

    1. La ecuación de la que obtenemos Φ es, precisamente: x² − x − 1 = 0, de donde: x² = x + 1. Basta sustituir x por Φ, que es una solución de dicha ecuación, para obtener la igualdad que se propone. También puede sustituirse cada miembro de la igualdad por el valor exacto de Φ y hacer las operaciones pertinentes para comprobar que se obtiene el mismo resultado.

    2. Φ² se obtiene sumando una unidad a Φ, por tanto tiene la misma parte decimal.

    3. Al dividir entre Φ y despejar se obtiene 1/Φ = Φ − 1, por tanto Φ y su inverso se diferencian exactamente en una unidad, por lo que también tienen la misma parte decimal.